In this article the mathematical formulation of Theta explained. Almost any broker calculates the daily theta value automatically, so there is no practical need to apply the function below yourself. However having understanding of the formula might help in understanding the dynamics of theta. Fear not, as we’ll break down the equation into simpler terms to make it accessible to everyone.

The Black-Scholes Model and Theta

To grasp the mathematical formulation of Theta, let’s look at the Black-Scholes model—an essential tool for pricing options. Within this model, Theta helps us quantify the rate at which an option’s value decreases over time.

The mathematical expression for Theta according the Black-Scholes model is given for both a call and a put option below, as the formula’s are slightly different for puts and calls. The symbol for theta is Θ (uppercase) or θ (lowercase).

Theta formula for a call option

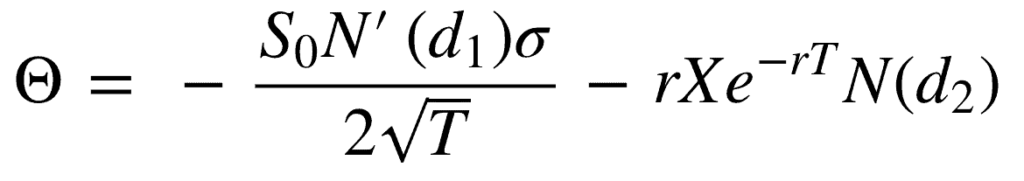
Theta formula for a put option

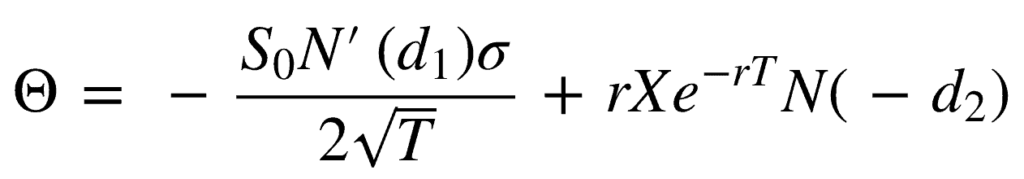
Now, let’s break it down into simpler components:

1. S: Represents the current price of the underlying asset. It could be a stock, index, or other tradable instruments.
2. N'(d1): This part represents the probability density function of a standard normal distribution. Don’t worry if it sounds complex; it helps us calculate the likelihood of the option reaching its strike price.
3. σ: Denotes implied volatility, which measures the expected magnitude of price fluctuations. Higher volatility leads to higher Theta values.
4. T: Refers to the time to expiration of the option. Theta is inversely related to time, meaning it increases as the expiration date draws near.
5. r: Represents the risk-free interest rate. It measures the return you could earn with no risk. As the interest rate rises, Theta tends to be higher.
6. K: Signifies the strike price of the option. It’s the price at which the option holder can buy or sell the underlying asset. Theta increases when the strike price is further from the current asset price.
7. N(d2): represents the cumulative distribution function of the standard normal distribution. It helps us calculate the probability of the option expiring in-the-money.

Differences in Theta for selling or buying an option

Now that we’ve broken down the equation, let’s understand its practical implications. Theta is usually expressed as a negative value for long options (buying) since their value declines over time. This means that as each day passes, the option loses a bit of its worth. It’s important for long option holders to be aware of Theta, as it represents the ongoing cost of holding the option.

On the other hand, short options sellers (selling) benefit from positive Theta. Time decay works in their favor, allowing them to profit from the erosion of an option’s value as time passes. Short option strategies often involve capturing the premium upfront and aiming to close the position before Theta significantly erodes the option’s value.

Congratulations on unraveling the mathematical formulation of Theta! By understanding this essential Greek parameter in options trading, you are better equipped to navigate the exciting world of option trading.

Disclaimer

The information provided on this website is for educational and informational purposes only. I am not a licensed financial professional, and the content presented here does not constitute investment advice. Engaging in option trading or any other financial activity involves risks, and there is a possibility of losing money. It is important to thoroughly research and understand the risks before making any investment decisions. Please consult with a qualified financial advisor or broker before engaging in any trading activities. The author and the platform shall not be held responsible for any losses incurred as a result of the information provided in this blog. By reading this blog, you acknowledge and accept the inherent risks associated with participating in the financial markets and agree to bear full responsibility for your own investment decisions.